Vectors for Game Physics

Vectors are the backbone of game physics. The Vec2 class gives you everything you need for 2D movement, collision response, and spatial calculations.

Creating Vectors

A Vec2 represents a point or direction in 2D space. You can create them with x and y components, or as a zero vector.

position = kn.Vec2(100, 200)
velocity = kn.Vec2(-3)  # (-3, -3)
zero = kn.Vec2()  # (0, 0)

Access components with .x and .y:

print(f"X: {position.x}, Y: {position.y}")

Basic Movement

The simplest physics is moving an object by adding velocity to position each frame. Multiply velocity by delta time to keep movement frame-rate independent.

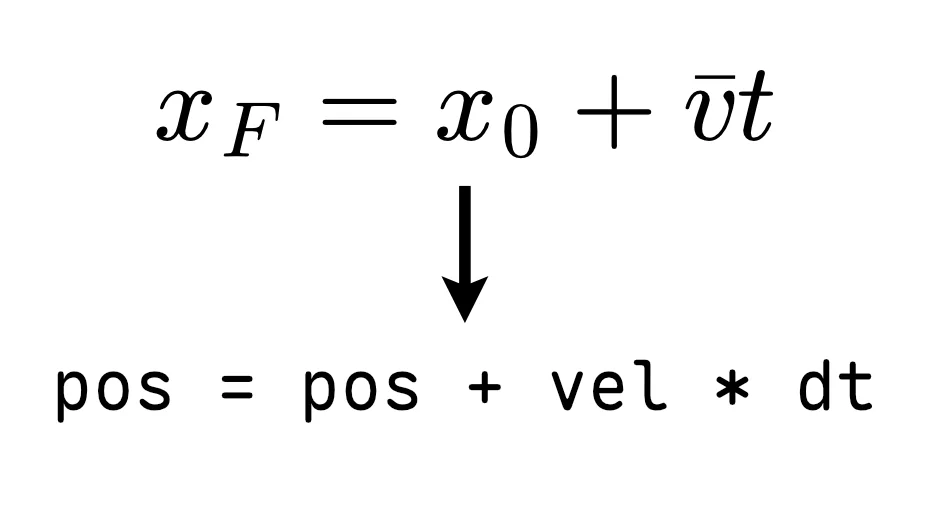
Velocity motion equation as code 
import pykraken as kn

kn.init()
kn.window.create("Movement Demo", (800, 600))

position = kn.Vec2(400, 300)
direction = kn.Vec2(1, 0)  # Moving right
speed = 200  # pixels per second

while kn.window.is_open():
    kn.event.poll()
    dt = kn.time.get_delta()

    # velocity = speed * direction
    # Optimization tip: Multiply the scalars first
    position += dt * speed * direction

    kn.renderer.clear("#222")
    kn.draw.circle(kn.Circle(position, 20), kn.color.WHITE)
    kn.renderer.present()

kn.quit()

Result:

Normalizing Vectors

A normalized vector (unit vector) has a length of 1. This is essential for consistent movement speed. Without it, diagonal movement is about 1.41x faster!

# Without normalization, diagonal is faster
direction = kn.Vec2(1, 1)  # length ≈ 1.414

# Normalize to get consistent speed
direction.normalize()  # new length = 1.0

# Now apply your desired speed
speed = 200
velocity = direction * speed

Use normalization whenever you need a pure direction without magnitude.

Dot Product

The dot product tells you how aligned two vectors are:

  • Positive: Same general direction
  • Zero: Perpendicular (90°)
  • Negative: Opposite directions
forward = kn.Vec2(1, 0)
to_target = kn.math.normalize(target_pos - my_pos)

alignment = kn.math.dot(forward, to_target)

if alignment > 0.7:
    print("Target is in front")
elif alignment < -0.7:
    print("Target is behind")
else:
    print("Target is to the side")

Cross Product (2D)

In 2D, the cross product returns a scalar indicating rotation direction. Useful for determining which way to turn to face a target.

a = kn.Vec2(1, 0)
b = kn.Vec2(0, 1)

# Positive, meaning b is counter-clockwise from a
cross = kn.math.cross(a, b)